Mon précédent article sur le modèle SIR était purement théorique. On m’a fait remarquer qu’une simulation numérique serait bien pour rendre concret les implications de ce modèle. C’est désormais chose faite et je vais vous exposer les résultats ici. Cet article sera sans équation pour le garder le plus accessible possible. Toutes les équations sous-jacentes sont dans l’article théorique. Vous pouvez télécharger le tableur ici. C’est possible de le modifier facilement vous-mêmes.
Présentation brève du modèle sans équation
Le modèle SIR est dit « compartimental » car la population est divisée en compartiments:
- Les personnes susceptibles d’être infectées (compartiment S)
- Les personnes infectées ( compartiment I)
- Les personnes remises de la maladie ( compartiment R)
Les gens du compartiment S ne peuvent aller que dans le compartiment I. Et ceux du compartiment I ne peuvent aller que dans le compartiment R. On ne compte pas explicitement les morts.
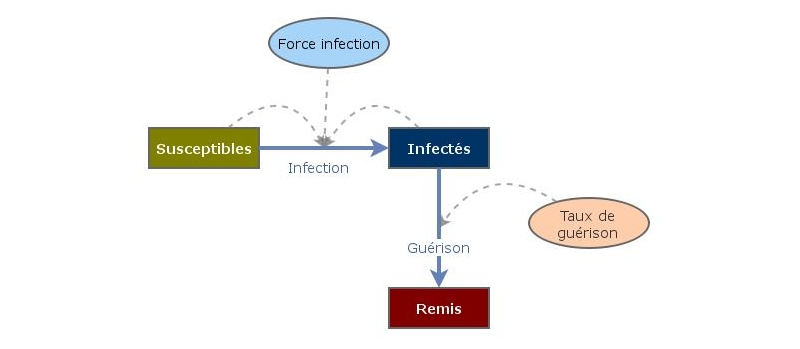
Nous avons besoin de trois valeurs de départ :
- La population totale. On prend la population française dans cette simulation donc 65 millions.
- La durée moyenne où on va considérer une personne comme contaminante. Pour des raisons pratiques, on va prendre la durée moyenne d’incubation qui est de 5 jours. C’est une simplification mais elle se justifie. Quand la personne ne ressent pas les symptômes, c’est là qu’elle va être contaminante. Une fois malade, la personne s’isole donc elle contamine beaucoup moins de monde. Cette durée de 5 jours correspond à ce qui se fait dans les simulations numériques en recherche sur le COVID-19. J’ai pris inspiration sur ce papier et cet autre travail de recherche.
- Le nombre de reproduction de base (le fameux \(R_0\) que l’on appelle \(\rho_0\) dans l’article précédent pour éviter la confusion avec le compartiment R). Il s’agit du nombre moyen de personnes contaminées par une personne infectée pendant toute la durée où elle est infectée. Elle est de 2,5 pour le COVID-19.
Le nombre de reproduction base représente les entrées dans le compartiment I pendant une période donnée. On ne peut pas comparer des nombres de reproduction de base de différentes maladies. Les durées de contamination par une personne infectée ne sont pas les mêmes. Pour pouvoir comparer, il faut calculer le nombre de personnes que contamine une personne infectée en une journée. Si on reprend les équations de notre modèle SIR, le nombre de personnes infectées par jour est multiplié par environ 1,3 en début d’épidémie. Je dis bien environ car en réalité ce nombre décroît comme on le verra plus tard.
Les résultats de la simulation
L’ampleur de l’épidémie peut être résumée par les statistiques suivantes
| Statistiques | Nombre | Nombre de jours | Pourcentage de la population |
| Personnes non infectées | 6112635 | 174 | 9.40 |
| Personnes contaminées | 58887365 | 174 | 90.60 |
| Pic épidémique | 16189408 | 69 | 24.91 |
On observe que 6 112 635 personnes vivant en France ne seront jamais atteint par le virus, soit 9,40% de la population. Tout le reste de la population a été contaminée. Le pic épidémique est atteint en 69 jours avec un nombre total de 16 189 408 personnes infectées ce jour là soit un quart de la population. Sachant que 15% des personnes infectées sont hospitalisées et qu’il y a 1% environ de décès, on imagine bien les dégâts catastrophiques si ce scenario se produisait.
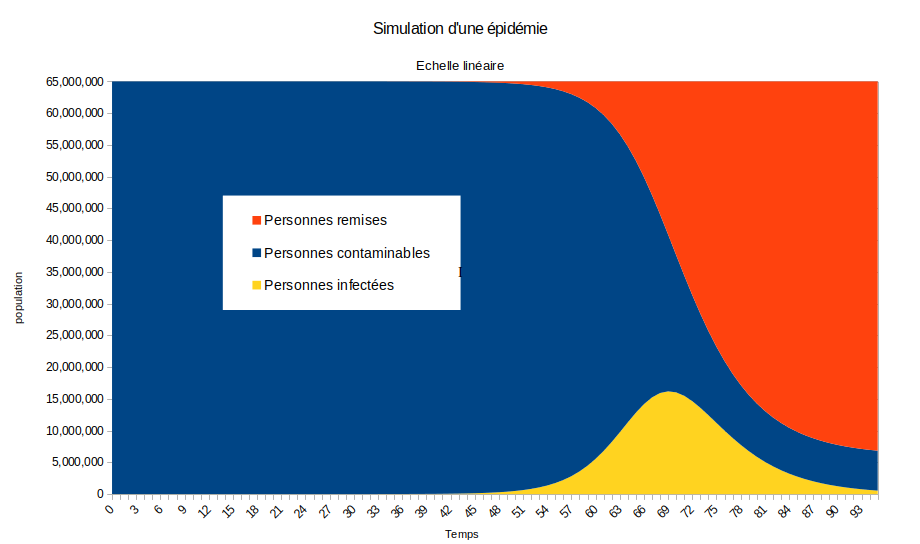
On peut aussi présenter ce graphique avec une échelle logarithmique. Les écarts ne sont plus en valeur mais en proportion. On peut plus facilement représenter l’évolution de l’épidémie.
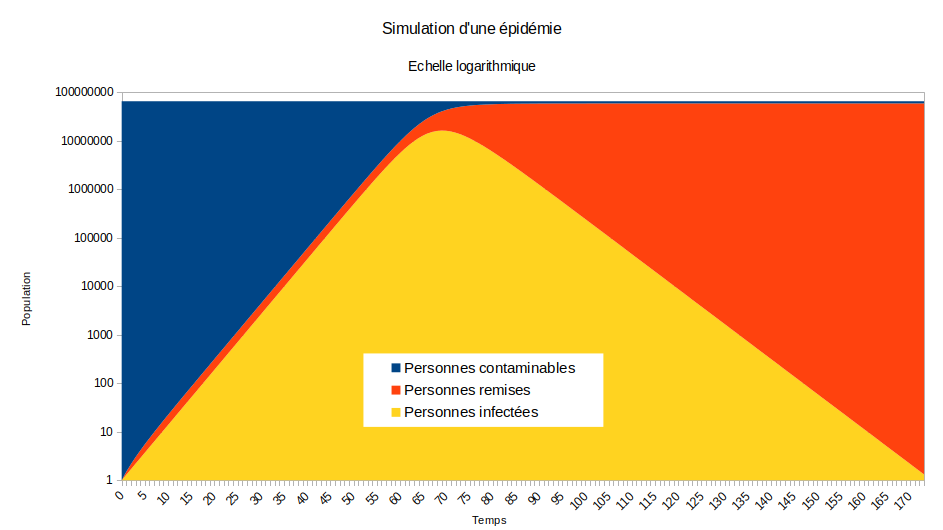
L’évolution du nombre de personnes infectées en forme de segment, sauf au sommet qui est arrondi, montre qu’on peut approximer le début de l’épidémie avec une fonction exponentielle. En gros, on peut multiplier par 1,3 (le facteur de reproduction de base) le nombre de personnes infectées en début d’épidémie tous les jours.
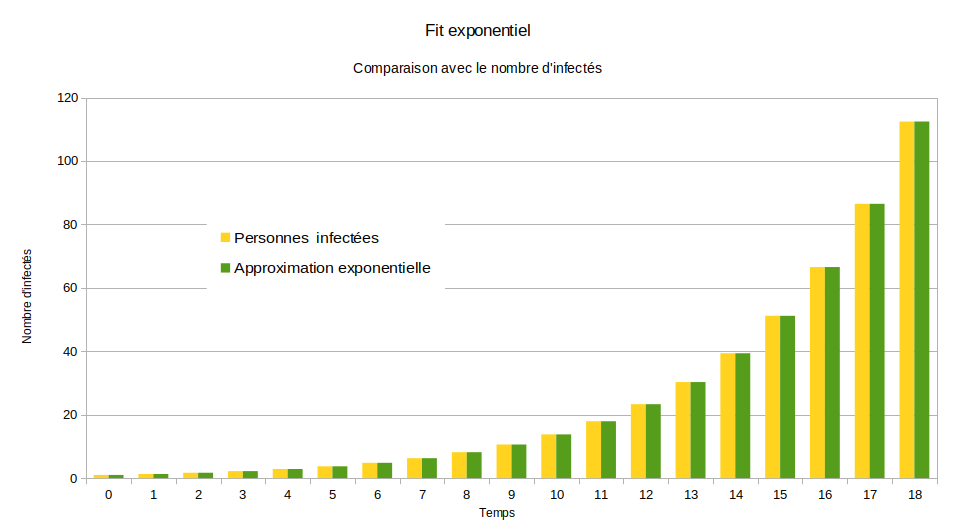
Néanmoins, la fonction exponentielle croit sans limite, ce qui n’est pas le cas de l’épidémie. La population est fixe. Il y a progressivement de moins en moins de personnes à infecter. Mécaniquement, cela freine l’expansion de l’épidémie jusqu’à ce que le pic soit atteint et que le nombre de personnes infectées décroît pour converger vers 0. Cette divergence est exprimée par le graphique suivant :
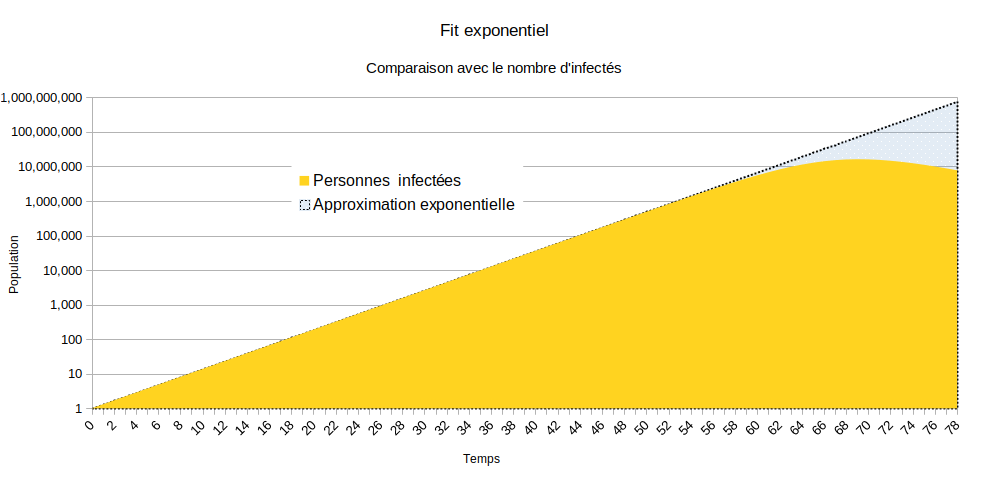
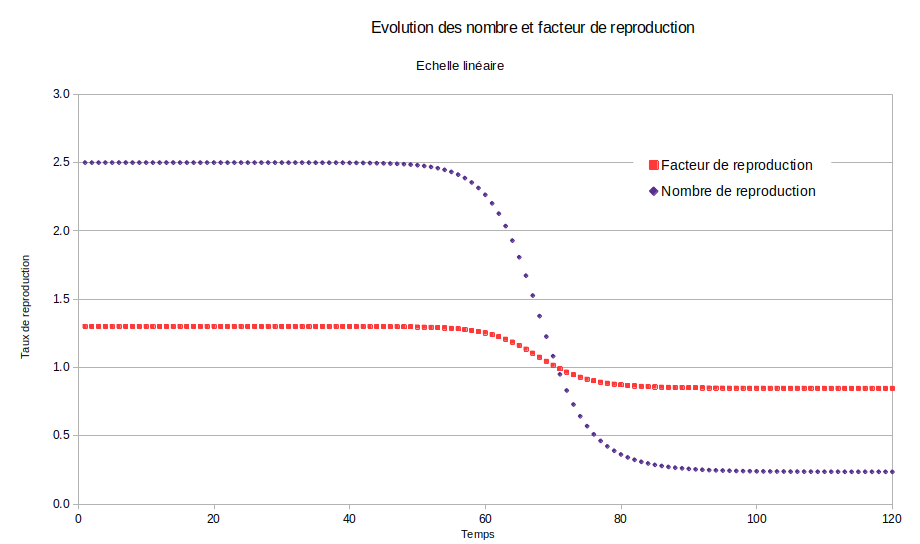
Le phénomène d’une épidémie n’est pas exponentielle à proprement parler. Les nombre et facteur de reproduction décroissent en fonction du taux. C’est juste qu’au début de l’épidémie, ils décroissent très lentement, comme le montre ce tableau:
| Facteur de reproduction | Nombre de reproduction | Nombre de jours |
| 1.3 | 2.5 | 0 |
| 1.29999999 | 2.49999996 | 1 |
| 1.29999999 | 2.49999994 | 2 |
| 1.29999998 | 2.49999992 | 3 |
| 1.29999998 | 2.49999988 | 4 |
| 1.29999997 | 2.49999984 | 5 |
On représente cette évolution des facteurs et nombre graphiquement ci-dessous :
Je voudrais attirer sur une limite de ce modèle SIR. Il y a une extrême sensibilité aux paramètres initiaux. Avec un nombre de reproduction de base, nous avons 58 887 365 de personnes contaminées. Avec un nombre de reproduction de 2,4, la simulation donne 57 966 860, soit 900 000 personnes en moins environ. Et avec une valeur de 2,6, on obtient 59 684 736 soit 800 000 de plus, l’agglomération toulousaine en gros.
Il est possible d’ajouter d’autres compartiments comme les décès et le nombre de personnes hospitalisées pour rendre le modèle SIR plus réaliste.

Cette flexibilité des modèles compartimentaux permet de les adapter pour modéliser les situations souhaitées. Neanmoins, comme le soulignent Chen Shen, Nassim Nicholas Taleb et Yaneer Bar-Yam dans une revue du modèle compartimental de l’épidémiologiste Neil Ferguson, les modèles SIR ne prennent pas en compte plusieurs caractéristiques du monde réel :
Celles-ci comprennent (1) des dynamiques locales interactives significatives et des restrictions de voyage qui ne peuvent pas être vues à partir de quantités agrégées ou de moyennes entre les emplacements géographiques, (2) des distributions non normales du nombre d’infections par personne (événements de super propagation) ainsi que la période d’infection, et (3) des valeurs dynamiques ou stochastiques de paramètres qui proviennent de variations dans l’échantillonnage des distributions ainsi que l’impact de l’évolution des efforts de réaction sociale.
Chen Shen, Nassim Nicholas Taleb et Yaneer Bar-Yam
Le 3e point est important car il souligne que le modèle SIR (notamment dans la version présentée ici) ne montre pas comment les individus réagissent à l’épidémie. Heureusement, il existe d’autres modèles pour pallier aux limites des modèles compartimentaux du type SIR.
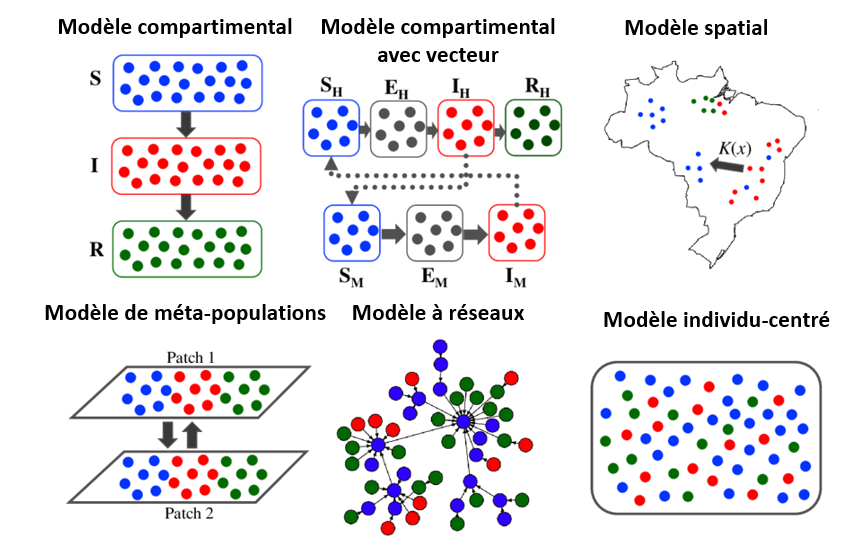
La présentation des modèles existants en épidémiologie dépassent le sujet de cet article. Je vous renvoie à cette vidéo de Thibault Fiolet qui a une super chaîne sur YouTube de nutrition et d’épidémiologie:
Views: 486