Cet article est le troisième chapitre d’une série d’article de vulgarisation du modèle SIR. Néanmoins, il peut se lire indépendamment des deux autres. Le premier chapitre est théorique et le deuxième présente les résultats de simulation pour la France. Ce troisième chapitre s’attarde sur la notion d’overshoot. Nous rappelons ici qu’il s’agit d’un modèle jouet à but pédagogique et pas d’un instrument fiable de prédiction.
Une des craintes en épidémiologie, c’est ce que l’on appelle l’overshoot. Ce phénomène désigne un état où le nombre de personnes atteintes par un agent pathogène (comme un virus ou une bactérie) est bien supérieur au seuil d’immunité collective. On mesure l’overshoot par la différence entre le nombre de personnes contaminées et le seuil d’immunité collective. Vous pouvez télécharger le tableur avec le modèle ici. Dans le chapitre précédent, nous avions les paramètres suivants pour simuler une épidémie de COVID-19 dans le but de modéliser la progression du virus SARS-Cov2 :
| Paramètres | Valeur |
| Population totale | 65 000 000 |
| Nombre de reproduction de base (\(R_0\)) | 2,5 |
| Durée moyenne de période contaminante | 5 jours |
Au vu de ces paramètres, le modèle donne un seuil d’immunité collective de 39 millions (soit 60% de la population française). Pourtant, la simulation donne 58 887 365 personnes infectées (soit 90,60% de la population française). L’overshoot est de 19 887 365 personnes, soit 30,60% de la population française. Ce phénomène d’overshoot est un des arguments contre la stratégie d’immunité collective. Miser dessus, c’est prendre le risque d’un nombre de personnes atteintes bien supérieures au seuil de l’immunité collective.
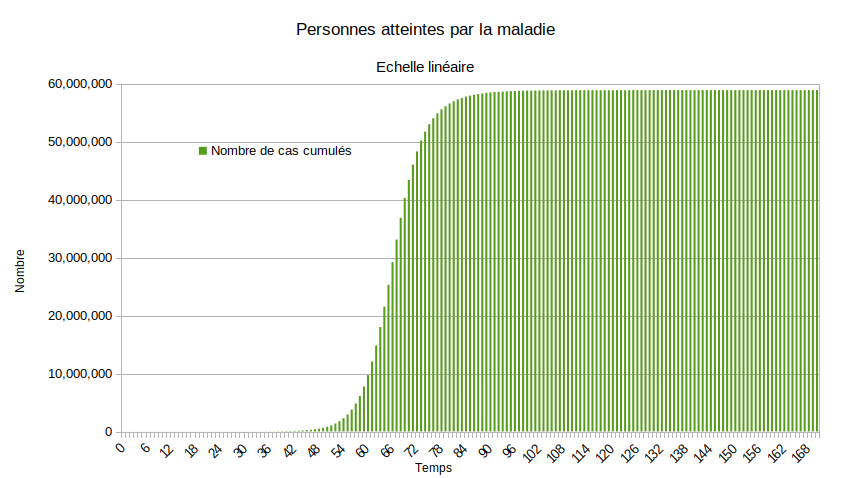
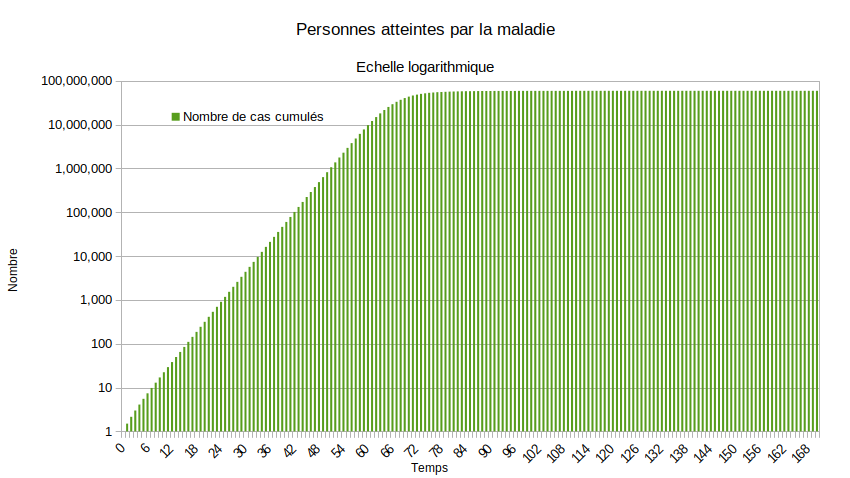
Qui sont les personnes contaminées dans le phénomène d’overshoot ?
Il y a deux facteurs. Premièrement, Au pic qui est le 69e jour, nous avons 16 189 408 de personnes contaminantes (24,91% de la population) et 40 307 505 (62,01% de la population). Au pic de l’épidémie, le seuil d’immunité collective est atteint. On a déjà un overshoot de 1 307 505 personnes. Cela s’explique par la progression multiplicative de l’épidémie. Dans le modèle utilisé ici et expliqué au premier chapitre, la progression d’une épidémie est multiplicative. Pendant la phase de progression de l’épidémie précédant le pic, le facteur de reproduction est d’environ 1,3. On multiplie tous les jours par environ 1,3. Je dis bien environ car en réalité ce nombre décroît très lentement sauf aux abords du pic où il décroît nettement plus fortement.
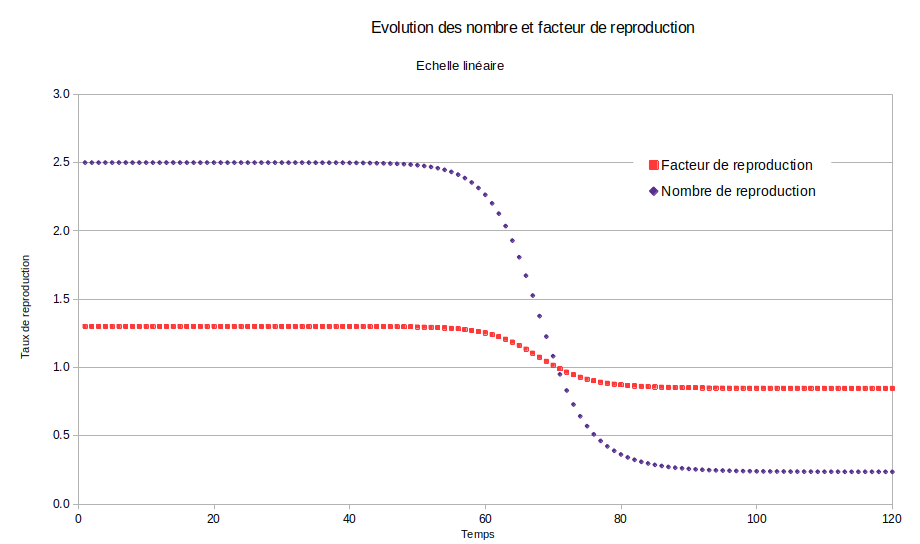
Du simple fait de la progression multiplicative, nous avons un overshoot de 1 307 505 personnes. Mais qui sont les 18 579 860 restants ? Ce sont les personnes atteintes pendant la phase décroissante de l’épidémie.
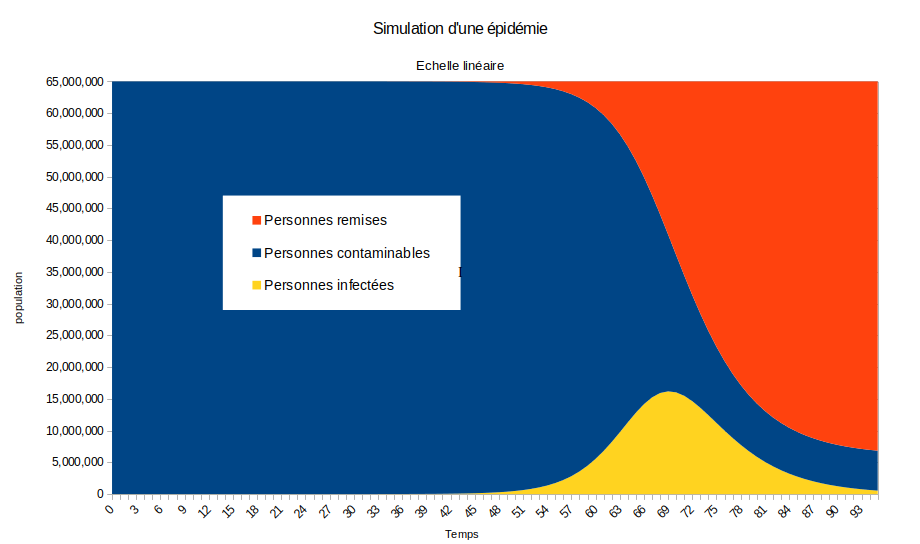
Cependant, nous pouvons nuancer l’overshoot et plus généralement les prédictions du modèle utilisé dans cet article. Le facteur de contamination (c’est le nombre de personnes contaminées par une personne contaminante) est constant. Ce n’est pas vrai parce que les gens réagissent à l’épidémie. Individuellement, ils prennent des mesures de précaution. Et même sans confinement, le gouvernement et les institutions peuvent sensibiliser aux gestes barrières. Enfin, il y a toujours le confinement comme ultime recours.
Néanmoins, les dynamiques décrites ici restent vraies tant que les mesures de reproduction sont supérieures à un. Ce qui est probable en cas de de levée du confinement.
Views: 479