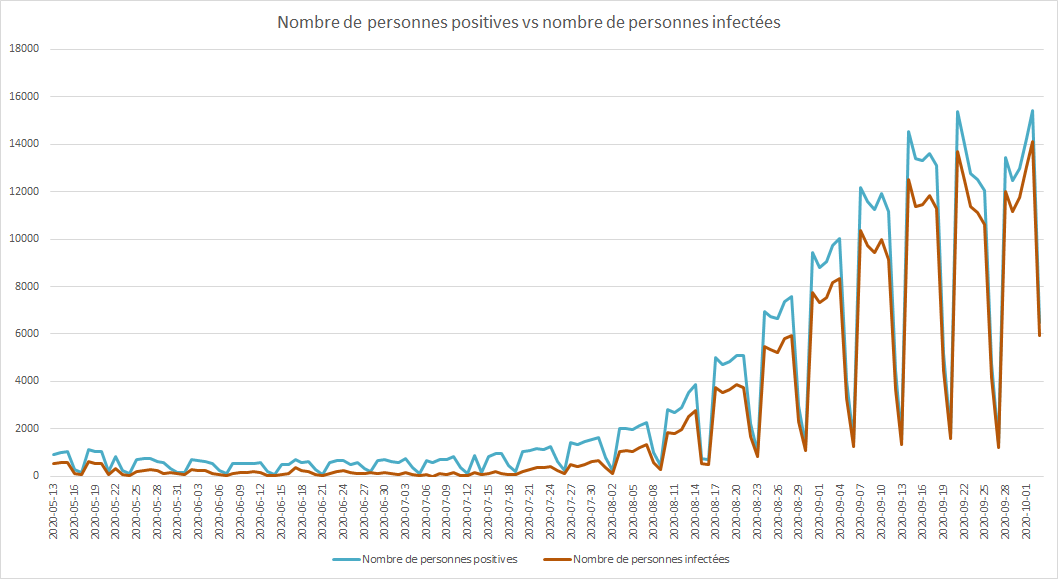
Il n’est pas rare d’entendre parler des faux positifs parmi les résultats des tests RT-PCR qui servent à dépister la présence du SARS-COV2, le virus responsable de la maladie dite du COVID-19. Le premier argument que l’on entend est qu’en raison de la faible proportion de malade (moins de 10% de la population), on teste surtout des gens sains et donc la probabilité d’obtenir un positif qui soit faux est plus forte que celle d’obtenir un positif qui soit vrai. Les probabilités bayésiennes nous montrent bien qu’une faible prévalence peut amener à un nombre important de faux positifs, comme je l’explique dans un autre billet. Le problème, c’est que l’on ne connaît pas directement le taux de prévalence. Le but de cet article est d’expliquer comment on peut calculer cette prévalence afin de calculer les valeurs prédictives des tests. L’intérêt est de pouvoir calculer au jour le jour le vrai nombre de personnes infectées ainsi que de voir l’évolution des faux positifs et négatifs, comme dans le graphique ci-dessous :

On peut voir que jusqu’à début août, les positifs sont majoritairement des faux. Le nombre de personnes infectées a continuer à augmenter alors que le nombre de faux positifs est resté relativement stable. On remarque aussi que le décollage du nombre d’infectés date du 20/07 environ.
Comment calcule-t-on ces valeurs ?
Pour autant, on peut le retrouver grâce à trois variables que l’on connaît :
- Le taux de positivité donné quotidiennement par Santé Publique France.
- La sensibilité du test: la probabilité d’être positif si vous êtes infecté. Selon wikipédia, elle est de 99% pour le test RT-PCR multiplex.
- La probabilité de faux positif qui est la probabilité d’être positif si vous êtes sain. Selon wikipédia, elle est de 2% pour le test RT-PCR multiplex.
Selon la formule des probabilités totales, on obtient :
Probabilité d’être positif = probabilité d’être positif sachant que l’on est infecté X probabilité d’être infecté + probabilité d’être positif sachant que l’on est sain X probabilité d’être sain
La probabilité d’être positif sachant que l’on est sain est la probabilité de faux positif. On peut réécrire cette formule de la façon suivante :
Probabilité d’être positif = sensibilité X probabilité d’être infecté + probabilité de faux positif X (1 – probabilité d’être infecté )
On obtient alors :
\(\text{Probabilité d’être infecté} = \frac{\text{Probabilité d’être positif – probabilité de faux positif}}{\text{sensibilité – probabilité de faux positif }} \)Calcul de la prévalence dans la population testée
On aura une probabilité d’être infecté (ou taux de prévalence) pour un taux de positivité compris entre la probabilité de faux positif et la sensibilité. Si tout le monde est sain, le nombre de positifs sera égal au nombre de faux positifs. Si tout le monde est malade, le nombre de positifs sera proportionnel à la sensibilité. Il est important de souligner que le taux de prévalence ne vaut que pour la population testée un jour donné. Cette valeur n’est pas généralisable à l’ensemble de la population française. Pour le 02/10, avec une valeur du taux de positivité de 9,8%, la prévalence est de 9%. Pour 156 961 personnes testées, ce jour là, 15410 étaient testées positives. Le nombre de personnes infectées est donc estimée à 14 123.
L’autre point intéressant est que la probabilité d’être infecté au sein de la population étudiée est une fonction linéaire croissante du taux de positivité. Ce dernier est donc un bon indicateur de tendance de la prévalence. Ce que l’on peut observer graphiquement :
Calcul du nombre de faux positifs
Vu qu’il y avait un nombre important valeurs du taux de positivité entre 1 et 2%, j’ai pris une valeur de 1% pour le taux de faux positif. Ce qui semble indiquer que le test RT-PCR est plutôt fiable pour détecter les personnes infectées. Bien que l’on teste plus de personnes qu’avant, il ne faut pas oublier que la hausse du nombre de cas positifs a été beaucoup plus forte que celle du nombre de personnes testées.
A part quand le taux de prévalence est faible, l’écrasante majorité des cas positifs actuellement sont réellement infectés. On observe au cours du temps une baisse du taux de faux positif :
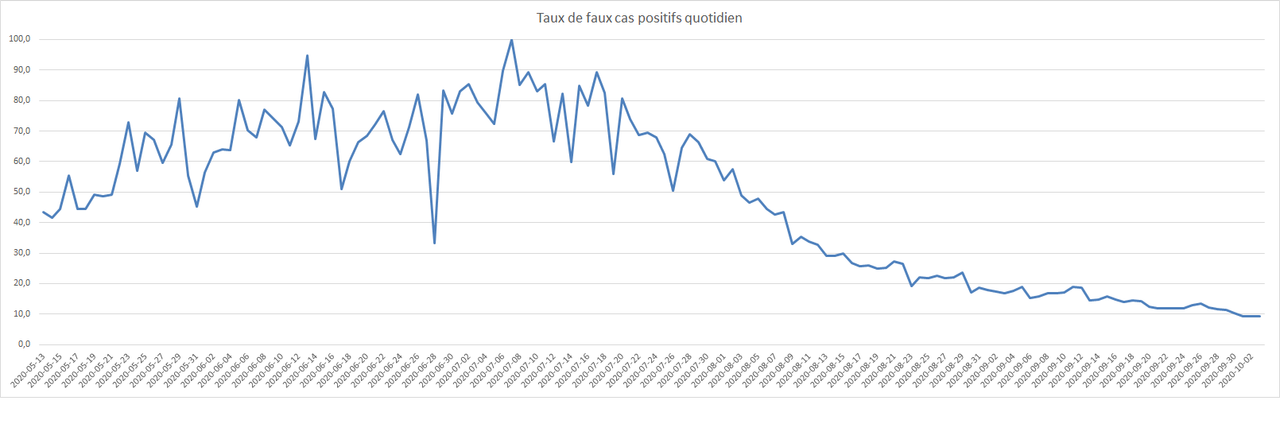
Le taux de faux positifs est très sensible pour de petites valeurs du taux de positivité d’où des oscillations importantes avant le mois d’août. Une fois que la seconde vague a prise, la variabilité du taux de positif est devenue moindre et a baissé en tendance. Quand le taux de positivité est supérieur à 2%, plus de la moitié des cas sont des vrais positifs. Or depuis le 3 août, ce seuil a été dépassé et le taux de positivité ne fait qu’augmenter. Avec un taux de positivité à 9,8% comme le 03/10, le taux de faux parmi les cas positif est seulement de 9,3%.
Il faut aussi prendre en compte les cas de faux négatifs. Toujours avec la formule de Bayes, on peut calculer les valeurs prédictive négative (très proche des 100%) et positive (90,7%) pour le 02/10. On peut ainsi calculer le nombre de personnes vraiment négative qui est de 141 422 et le nombre de personnes vraiment positives qui est de 13 982 :
| Mesure | Valeur | Pourcentage |
| Nombre de personnes testées | 156 961 | 100 |
| Nombre de personnes vraies positives | 13 982 | 8,9 |
| Nombre de personnes faussement négatives | 129 | 0,1 |
| Nombre de personnes vraies négatives | 141422 | 90,1 |
| Nombre de personnes faussement positives | 1428 | 0,9 |
Le deuxième argument avancé est que le test RT-PCR mesure la présence du virus et non si la personne est contagieuse. Les biologistes mesurent aussi la quantité de traces du virus présentes. D’où un débat très animé sur le seuil à placé pour écarter les personnes infectées avec une trop faible présence virale détectée du reste des autres cas positifs. Cela ne change pas le fond du problème. Les personnes qui ont sur elles de faibles présences de trace du virus ont bien été infectées par le passé. Si en testant quotidiennement, on observe un nombre de plus en plus grand de ces personnes, c’est bien que dans ce cas l’épidémie progresse. D’un point de vue statistique, on ne peut pas ignorer cette information. Au niveau individuel, c’est aux médecins et aux biologistes d’évaluer si une personne testée positive est contagieuse ou non.
Views: 462